728x90
표준정규분포표는 표준정규분포에 대한 누적분포함수 $\Phi(Z_\alpha)$ 값을 미리 계산 해놓은 표로, 정규분포의 확률을 쉽게 계산하기 위해 사용한다.
$(1-\alpha)$ 분위수
$Z \sim N[0,1]$일 때, $P[Z<c]=1-\alpha$를 만족하는 $(1-\alpha)$ 분위수 c를 $Z_\alpha$로 표기한다.
$\Phi(c)=P(Z<c)= \int_{-\infty}^c f(Z)dz$
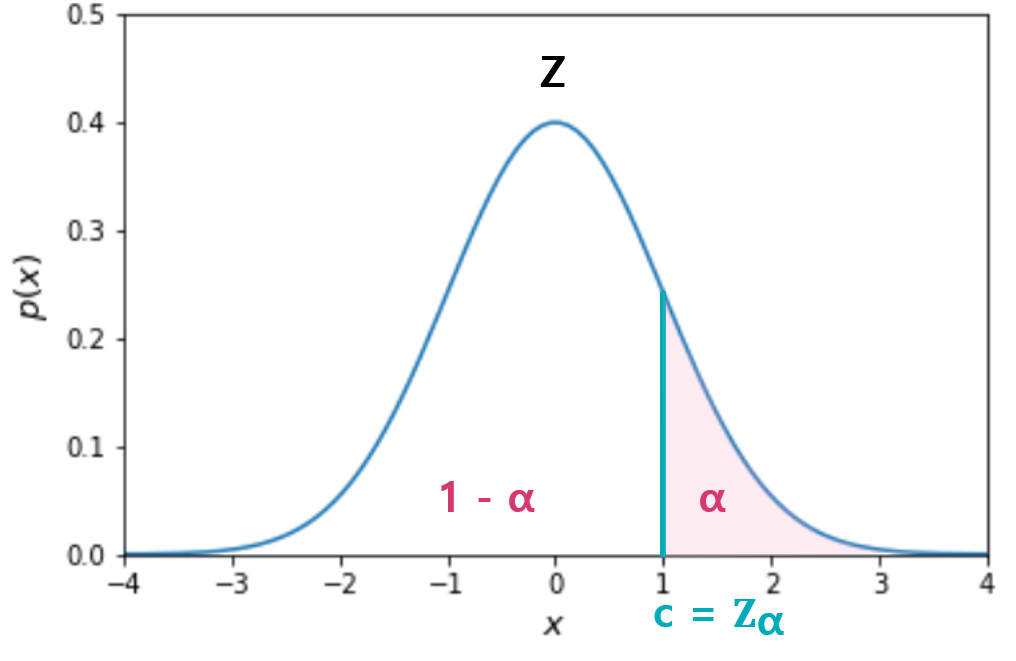
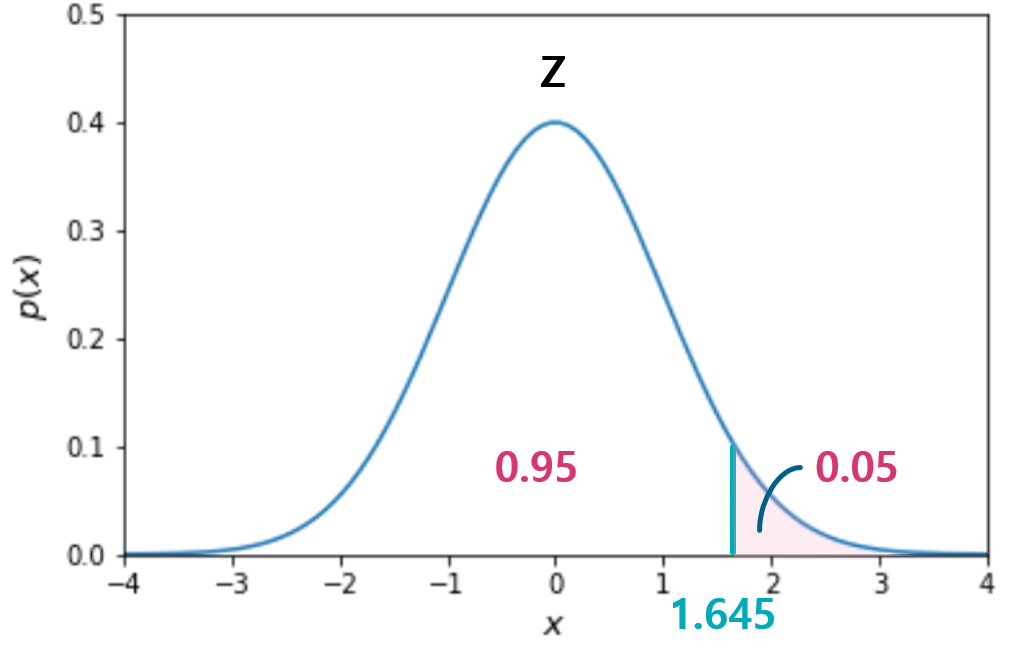
이 중 가장 자주 쓰이는 분위수는 0.05, 0.01 등이며, 이들의 누적확률은 다음과 같다.
- $P(Z≤1.645)=0.95$
- $P(Z≤1.96)=0.975$
- $P(Z≤2.326)=0.99$
- $P(Z≤2.576)=0.995$
표준정규분포표
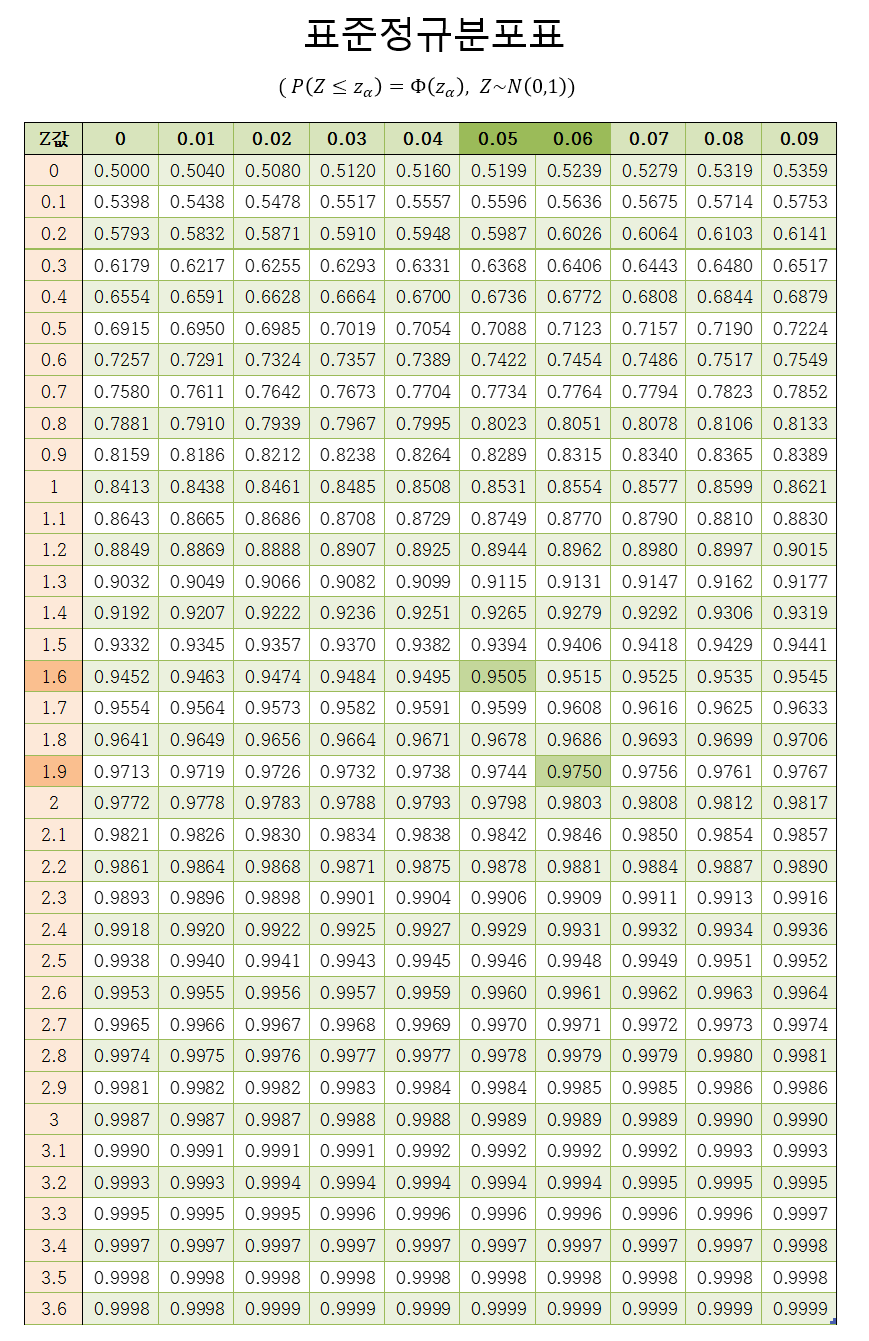
표준정규분포표 보는 법
표준정규분포는 정규분포의 평균이 0, 분산이 1인 특수한 경우로, "밀도함수의 곡선 아래 면적"으로 어떤 구간에 대한 확률을 구할 수 있다.
$Z_{0.05}$ 즉 0.95분위수인 값을 찾고자 하면, 표에서 0.95를 먼저 찾은 뒤 이에 해당하는 행의 이름 1.6과 열의 이름 0.05을 더해 누적확률 값이 1.65임을 볼 수 있다.
'IT > 통계' 카테고리의 다른 글
| 선형 회귀 분석 예시로 쉽게 이해하기 (0) | 2020.09.30 |
|---|---|
| 귀무가설 대립가설 개념 쉽게 이해하기 (0) | 2020.09.24 |
| 95% 신뢰구간 공식 쉽게 이해하기 (0) | 2020.09.24 |
| 정규분포 정의와 표준정규분포로 표준화 하는 방법 (0) | 2020.09.08 |
| 베이즈 정리 예시로 쉽게 이해하기 (0) | 2020.08.27 |



